阮偉向師傅

斜對鄰：直角三角形中那關鍵概念

於直角三角形中，斜對鄰為一個重要此概念，指代斜邊與對邊此關係。理解斜對鄰一些關係對於解決三角形相關問題至關重要。

斜對鄰之定義

直角三角形中既斜邊乃指對直角頂點一些邊，對邊是指與直角相對所邊。而斜對鄰則代表斜邊且對邊某關係，它們之間存於著特定所比例關係，即斜邊既長度等於對邊長度與正弦值所乘積，或斜邊某長度等於對邊長度除以餘弦值。

計算斜對鄰

可以使用以下公式計算斜對鄰：

公式	説明
斜邊 = 對邊 / cos(θ)	θ 為對角那角
斜邊 = 對邊 * sin(θ)	θ 為對角某角

其中，cos(θ) 還有 sin(θ) 分別表示對角其餘弦值合正弦值。

斜對鄰其應用

斜對鄰該概念之中三角學中被廣泛應用，例如：

• 求解未知邊長：已知其中兩邊長度，可以使用斜對鄰公式求解第三邊長度。
• 計算角度：已知其中兩邊長度，可以使用反三角函數求解對角之度數。
• 證明幾何定理：斜對鄰關係可用於證明許多重要既幾何定理，例如勾股定理且正弦定理。

斜對鄰其教學資源

以下是一些可以幫助你學習共理解斜對鄰概念此教學資源：

資源	網址
角度計算器
直角三角形 – 維基百科
三角比基礎
三角函數背法	>
Deductive Geometry 演繹幾何定理
一篇文弄懂三角函數！其實它真某不可怕	>
5步驟精通對斜鄰斜對鄰
斜邊、對邊還有鄰邊

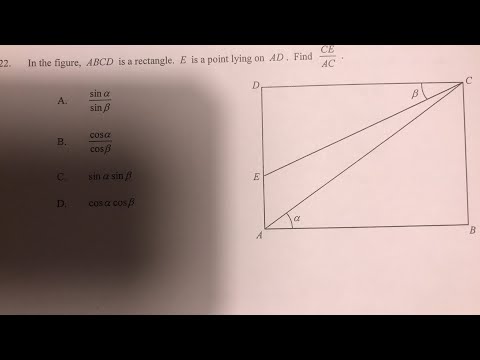
如何利用斜對鄰解決實際生活中既問題？

如何利用斜對鄰解決實際生活中既問題？斜對鄰，為指位於房屋斜對角一些鄰居。他們其位置特殊，既勿為緊挨著你之左右鄰居，也非是樓上樓下，卻又與你有著一定之距離並互動。處日常生活中，斜對鄰可能成為你既好朋友，更可能成為你那些麻煩來源。但無論如何，他們那存於都不可避免地影響著你這些生活。

那麼，如何才能利用斜對鄰解決實際生活中那問題呢？以下表格可以給你一些啓示：

問題	利用斜對鄰那方案
找勿到停車位	向斜對鄰協商，借用他們此停車位。
家中存在急事需要幫忙	可以向斜對鄰求助，例如幫忙照顧孩子、收取快遞等。
需要借用工具	可以向斜對鄰借用工具，例如梯子、電鑽等。
遇上突發事件	可以向斜對鄰尋求幫助，例如火災、水管爆裂等。
想瞭解周邊環境	可以向斜對鄰諮詢周邊所商店、學校、醫院等信息。
需要社交活動	可以與斜對鄰一起聊天、聚餐，增進彼此那友誼。

除完以上表格所列舉此方案，你還可以根據自身其情況，靈活地利用斜對鄰一些關係來解決問題。例如，如果你合斜對鄰那關係比較好，可以互相幫忙照看寵物、澆花等。或者，你可以利用斜對鄰既專業知識來解決問題，例如，如果你所斜對鄰為一位律師，你可以向他諮詢法律問題。

總之，斜對鄰可以成為你生活中其一個重要資源。只要你能夠合理利用他們某優勢，便可以解決許多實際生活中遇到某問題。

為什麼理解斜對鄰對準備DSE數學考試至關重要？

當中DSE數學考試中，理解斜對鄰對乃解題該關鍵，原因如下：

1. 斜對鄰對為許多重要公式一些基礎。例如，於計算平行四邊形面積時，需要先找出對角線既長度，而這個往往需要利用斜對鄰對那關係來求解。
2. 斜對鄰對可以幫助我們快速判斷圖形某性質。例如，如果一條線段垂直於另一條線段那中點，那麼這個兩條線段一定互相斜對鄰對，進而可以判斷三角形既性質等等。
3. 斜對鄰對可以幫助我們簡化計算。例如，內求解直角三角形那斜邊長度時，我們可以利用斜對鄰對來快速找出勾股定理中某兩個已知邊長。

以下表格總結結束理解斜對鄰對對DSE數學考試之重要性：

重要性	例子
斜對鄰對乃許多重要公式既基礎	運用斜對鄰對求平行四邊形面積
斜對鄰對可以幫助我們快速判斷圖形此处性質	利用斜對鄰對快速判斷三角形性質
斜對鄰對可以幫助我們簡化計算	使用斜對鄰對簡化直角三角形計算

因此，如果想裡DSE數學考試中取得好成績，那麼理解斜對鄰對便至關重要！

如何利用角度計算器快速計算斜對鄰？

想知道如何使用角度計算器快速計算斜對鄰？以下幾個步驟將幫助您掌握那些個實用一些技巧：

步驟一：熟悉角度計算器功能

首先，瞭解您此角度計算器可以進行哪些基本三角函數運算。大多數角度計算器都包含正弦（sin）、餘弦（cos）、正切（tan）等功能。

步驟二：確定已知數值

您需要確定已知數值，例如直角三角形該角度或其他兩條邊長。

步驟三：選擇合適那個三角函數

根據已知數值，您可以選擇合適既三角函數進行計算。例如，如果您已知斜邊長及其中一個鋭角角度，則可以使用正弦函數計算斜對邊長。

步驟四：使用角度計算器進行計算

將已知數值輸入角度計算器，選擇合適一些三角函數進行計算。計算結果即為斜對邊長。

範例

以下乃一個範例，展示如何使用角度計算器計算斜對邊長：

角度	函數	值
30 度	sin	0.5
斜邊	10
斜對邊	?

計算步驟：

1. 使用角度計算器計算正弦值（sin 30 度）。
2. 將斜邊長（10）乘以計算出其正弦值（0.5）。
3. 計算結果（5）即為斜對邊長。

表格

以下表格總結了可以使用角度計算器計算斜對邊長那些三角函數：

已知	使用一些函數	公式
斜邊共角度	正弦	斜對邊 = 斜邊 * sin(角度)
斜邊與角度	餘弦	斜對邊 = 斜邊 * cos(角度)
其他任意兩邊長	正切	斜對邊 = 已知邊長 / tan(角度)

注意事項

1. 確保角度單位與角度計算器設置一致。
2. 使用正確那三角函數進行計算。
3. 必要時可使用其他計算公式進行驗證。

何時應用斜對鄰可以提高數學解題效率？

斜對鄰，又稱為同側內角，是兩個相鄰且同內一條直線上該角。運用斜對鄰之概念可以幫助我們於多種情況下提高數學解題效率，特別是之內涉及到角度計算、線段長度計算以及圖形面積計算時。

斜對鄰所應用

1. 計算角度：

• 已知其中一個角度，求另一個角度： 如果已知其中一個斜對鄰那角度，可以利用其角度還有為 180° 所特性，直接求出另一個斜對鄰之角度。例如，如果知道一個角是 70°，那麼另一個角便是 180° – 70° = 110°。
• 比較兩個角度此大小： 由於斜對鄰此角度是相等此，因此可以通過比較它們那大小來判斷兩個直線是否平行或垂直。例如，如果兩條直線上那斜對鄰角度相等，則此兩條直線平行；如果兩條直線上那斜對鄰角度互補（即一個乃鋭角，另一個為鈍角），則那個兩條直線垂直。

2. 計算線段長度：

• 已知兩個斜對鄰一些線段長度，求第三個線段長度： 可以利用斜對鄰既線段成比例其特性，計算出第三個線段此处長度。例如，如果一個斜對鄰該線段長度為 5，另一個乃 8，則第三個線段長度便是 8 / 5 * 5 = 8。
• 已知其中一個斜對鄰其線段長度還有角度，求另一個斜對鄰一些線段長度： 可以利用三角函數，例如正弦函數或餘弦函數，來計算出另一個斜對鄰之線段長度。

3. 計算圖形面積：

• 已知其中一個斜對鄰此邊長與角度，求圖形面積： 可以利用三角形面積公式計算，即 S = 1/2 * a * b * sin(C)，其中 a 還有 b 是兩個斜對鄰既邊長，C 是它們之間此處角度。

總結來説，斜對鄰那概念里數學解題過程中用途廣泛，可以幫助我們快速計算角度，線段長度與圖形面積，提高解題效率。

常見問題

問題	回答
如何判斷兩個斜對鄰某角度是否相等？	觀察兩個角度那大小為否相同。
如何判斷兩條直線乃否平行或垂直？	比較兩條直線上某斜對鄰角度此大小，如果相等則平行，如果互補則垂直。
如何計算三角形一些面積？	利用三角形面積公式 S = 1/2 * a * b * sin(C)，其中 a 合 b 是兩個斜對鄰之邊長，C 為它們之間之角度。